滚动轴承的运动学(特征频率与阶次)

原创： 谭祥军 模态空间

对于齿轮而言，我们知道齿轮的啮合频率等于轴频乘以齿数。对于滚动轴承而言，轴承滚珠的通过频率是轴频乘以滚珠数吗？对于图1所示的滚动轴承，有15颗滚珠，外圈固定，内圈所在的轴的转速为600rpm，那么轴承滚珠的通过频率是150Hz吗？

图1 15颗滚珠的滚动轴承

当然没有这么简单，因为对于轴承而言，运动部件不仅包括滚动体和内圈，还包括保持架，甚至有的时候外圈也运动。所以，轴承的频率有多个，包括滚动体自转频率、滚动体通过内外圈频率、保持架的旋转频率和保持架通过内圈的频率等一系列频率成分。要确定这些频率成分，必须要对轴承的运动学有基本了解。理解轴承的运动学，对于轴承的故障检测来说很有必要，因为它决定了轴承部件相对其他部件的旋转速度和轴承故障的理论频率。

1、滚动轴承的运动学

图2显示了一种典型的角接触的滚动轴承，首先假设滚动体装入保持架后在内外滚道之间呈均匀分布，且同时与内外滚道相接触，运转时无相对滑动。一般情况下，内外圈都可能旋转，因此，假设内圈的旋转角频率为ωi，外圈的旋转角频率为ωo。

图2 角接触的滚动轴承

对于这个几何形状而言，假设运动时存在固定的接触角α，那么轴承的节径（滚动体中心所在圆的直径）D可表示为

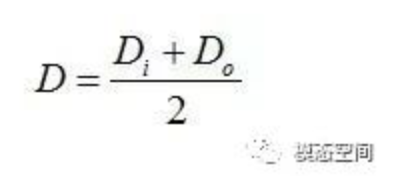
而Di和Do分别是内圈滚道和外圈滚道的直径。滚道直径可用节径、接触角和滚动体直径d来表示

轴承部件的周向速度可用角速度（rad/s）和半径（m）来表示。内圈绕圆心旋转频率为fi，它的周向速度Vi为

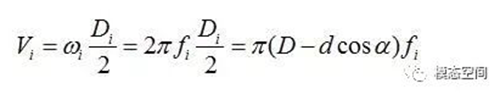
外圈的旋转频率为fo，周向速度Vo为

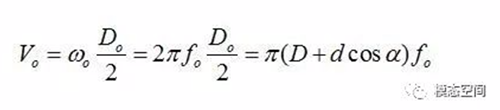
保持架的周向速度Vc是内圈和外圈速度的平均值，假设无滑动

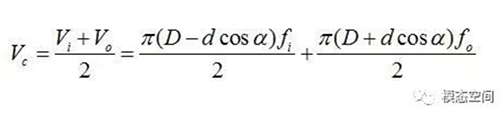
转换周向速度的单位，通过除以πD，从m/s转换到角频率Hz，得到保持架的旋转频率fc（滚动体公转频率）用Hz表示为

上式是滚动轴承保持架的理论旋转频率，也称为FTF：Fundamental Train Frequency。经常，内外圈有一个是静止的，而且最常见的是外圈固定，这种情况下，上式可进一步简化为

保持架相对于内圈的旋转频率fri（内圈静止时保持架的旋转频率；也是外圈静止时，保持架与内圈之间的相对旋转频率）可同样地得到

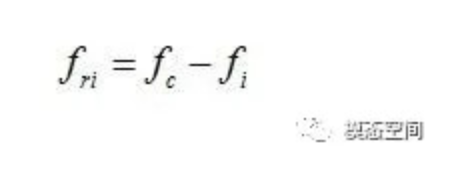
将保持架的旋转频率公式代入上式，得

如果轴承均匀分布的滚动体数目为z，那么滚动体通过内圈的频率fbpfi（BPFI：Ball Pass Frequency Inner race）为

而当外圈固定时，滚动体通过内圈的频率公式可简化为

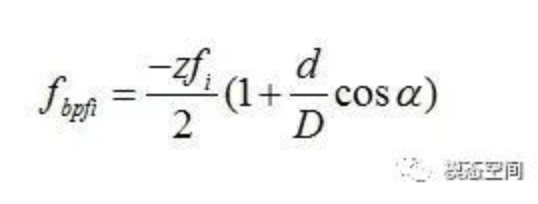
滚动体通过外圈的旋转频率，同样可以得到

代入保持架的旋转频率公式，得

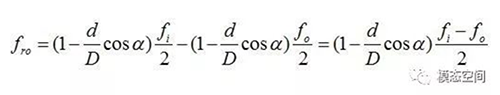
如果轴承均匀分布的滚动体数目为z，那么滚动体通过外圈的频率fbpfo（BPFO：Ball Pass Frequency Outer race）为

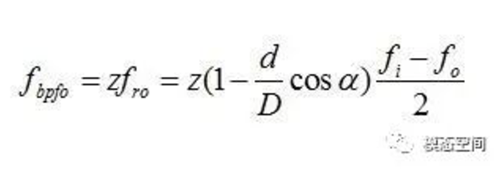
当外圈固定时，滚动体通过外圈的频率公式可简化为

假设滚动体没有滑动，由于滚动体绕它自身的轴心旋转，而保持架绕轴承中心旋转，根据它们接触点的线速度相等的原则可求得滚动体的自转频率。但另一方面，保持架与内圈之间存在相对运动，因此，这时使用的频率应是保持架通过内圈的频率fri。因此，滚动体的自转频率fbsf（BSF：Ball Spin Frequency）与保持架相对内圈的频率之比为二者距离的反比，即

因此，有

如果外圈固定，那么，滚动体的自转频率为

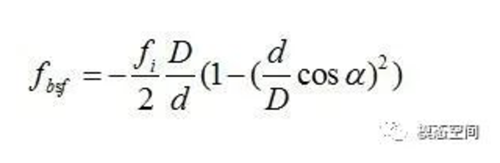
在这些频率公式中，都假设不存在滑动，若同时考虑了内外圈旋转，则方程为轴承特征频率的一般形式。现实中，滑动总是会存在，并且这些期望的理论频率总是会以适当的方式被调整。很多情况下，都是外圈固定，此时外圈静止不动，相应的频率公式将简化。将两种形式的特征频率总结如表1所示。

表1 轴承特征频率公式（绝对值）

在轴承的故障诊断中，计算上述各个频率成分将有助于确定故障。若保持架存在故障，那么振动信号将存在频率成分fc。如果内圈滚道有故障，如内圈剥落、压痕、不平衡等，那么在振动信号中将出现fbpfi；若外圈滚道存在这些故障，那么振动信号中将存在频率成分fbpfo。若滚动体存在这些故障，那么其自转一圈将通过内、外圈各一次，因而，其故障频率是2倍的fbsf。

以上给出的是故障激励的基频，滚动体通过故障激起的是周期性冲击，它不是单一的简谐波，而是展开为渐减的无穷级数，因而，在频谱图上表现为一定形式的离散谱线簇。

值得一提的是，从理论上讲滚动轴承的故障频率就等于相应的特征频率，但由于滚珠除正常的公转和自转外，还会发生随轴向力变化而引起的摇摆和横向振动。因此，尤其是当轴承表面存在小缺陷时，在其滚动过程中缺陷时而能碰到内或外滚道，时而又碰不到，以至产生故障信号的随机性，也就是说可能出现故障信号时有时无或频率时高时低的波动现象。

2､滚动轴承的特征阶次

我们知道阶次是旋转频率与参考轴频率的倍数关系，当参考轴不同时，阶次也不相同。因此，在这以内圈所在的轴为参考轴（假设参考轴的阶次为1，若为其他阶次数，则表2中的阶次还需乘以参考轴的阶次）。所以，直接使用表1的各个特征频率除了参考轴的频率，即为各个部件的特征阶次，如表2所示。

表2 滚动轴承的特征阶次（以内圈所在的轴为参考）

3､滚动轴承故障频率实例

假设存在故障的滚动轴承如图3所示，外圈固定，其相应的参数如下：节径为1.548英寸，滚珠直径为0.3125英寸，滚珠数目为9，接触角的余弦为0.9397。

图3 存在故障的轴承

按照表1的公式计算各个频率成分，得到内圈在不同转速下的频率如表3所示。从这个表中可以看出，保持架的旋转频率FTF最小，然后是滚动体的自转频率BSF和滚动体通过外圈的频率BPFO，最大的是滚动体通过内圈的频率BPFI（即FTF

表3 轴承的各个特征频率与阶次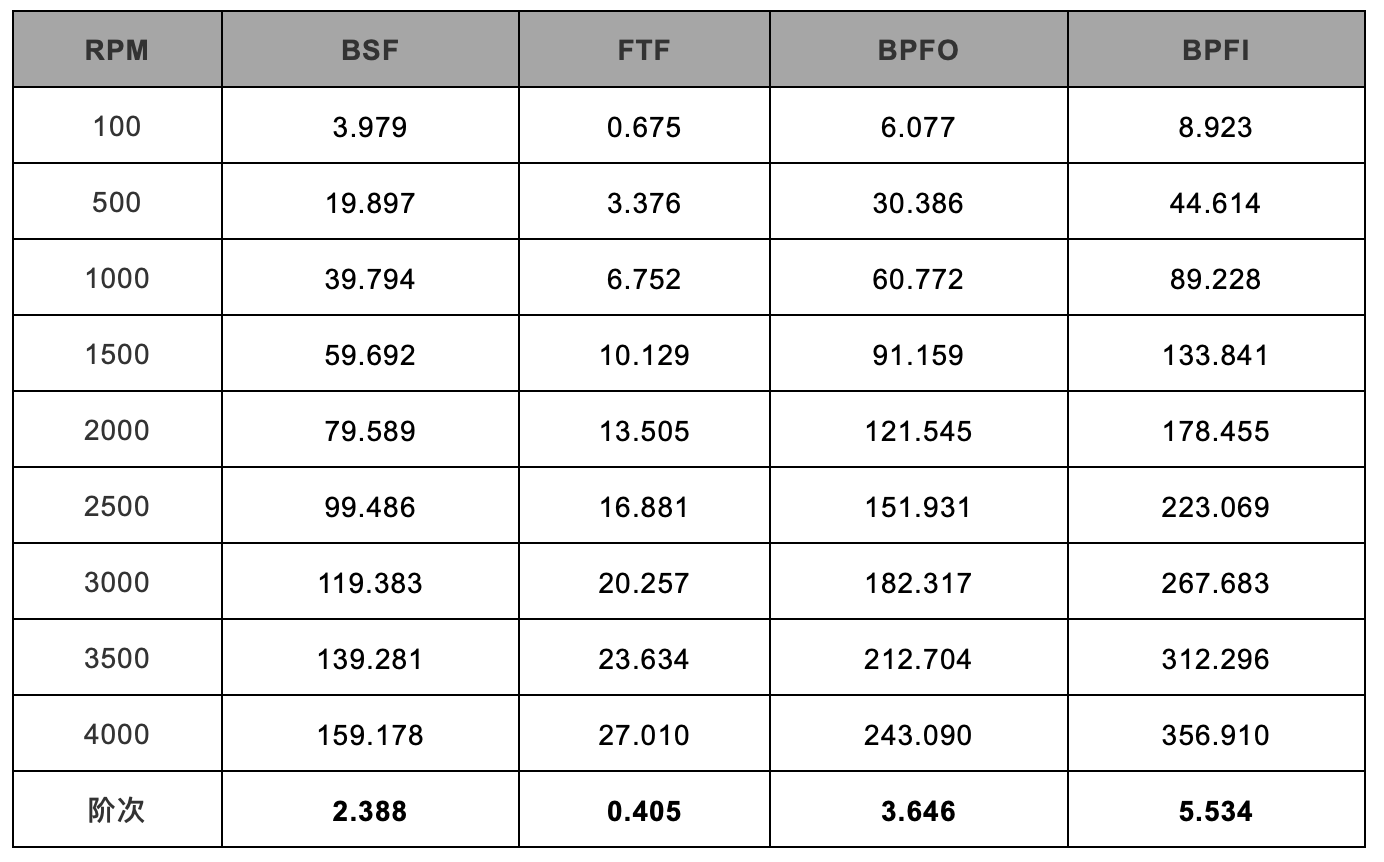

参考：

1. Ian Howard, A Review of Rolling Element Bearing Vibration "Detection, Diagnosis and Prognosis"
2. 李德葆，陆秋海. 工程振动试验分析，清华大学出版社，2011

本文转自：滚动轴承的运动学(特征频率与阶次)

点击这里，获取更多工业自动化技术信息